Gyroscope

This is a simple tutorial example of a driven dissipative dynamical system, which exhibits a period doubling route to chaos. I investigated this system back in 1991 as part of a practical training.
 

The System Route to Chaos The Attractor Animations

The System

The investigated system is a driven gyroscope [1]. Its potential is given by: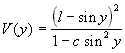

l,c - constants of the potential

It is modeled with the following differential equation:

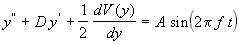
d.h.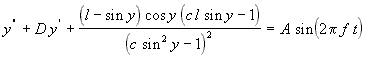


D - damping constant
A - amplitude of the driving force
f - frequency of the driving force
 

• The gyroscope is driven by an external harmonic force with an amplitude A and frequency f.
• It is a dissipative system because of the damping term D y'.
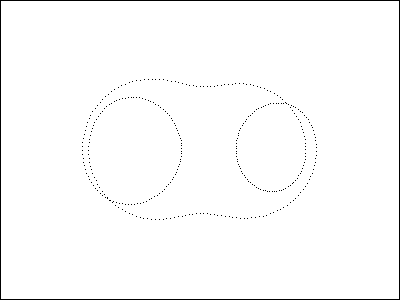
• The potential V for l = 0.5 and c = 0.5 looks like:

• For the numerical simulation a simple Runge-Kutta-scheme is used.

Route to Chaos

The system exhibits a period doubling route to chaos while changing the amplitude of the driving force.

The solution for small amplitudes of the driving force has the same period as the driving force. Therefore the Poincare section shows only one point:

Parameter: A = 0.23, f = 1, D = 0.1, c = 0.5, l = 0.5

Map of (y'(t), y(t))

Poincare section

By enlarging the amplitude of the driving force to A = 0.24 a period doubling bifurcation occurs. The system has the double period of the driving force (two points in the poincare section):

Parameter: A = 0.24, f = 1, D = 0.1, c = 0.5, l = 0.5

Map of (y'(t), y(t))

Poincare section

By enlarging the amplitude of the driving force to A = 0.25 the next period doubling bifurcation occurs:

Parameter: A = 0.25, f = 1, D = 0.1, c = 0.5, l = 0.5

Map of (y'(t), y(t))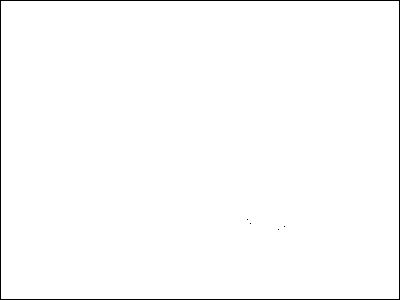

Poincare section

 

Enlarging the driving force further leeds to more period doubling bifurcation until the system exhibits a chaotic state by A = 0.255:

Parameter: A = 0.255, f = 1, D = 0.1, c = 0.5, l = 0.5

Map of (y'(t), y(t))

Poincare section [Click to enlarge]

For higher amplitudes of the driving force one can find so called periodic windows, where the solution is again periodic. E.g. at A = 0.5 the system is periodic with a period three times of the driving force's one:

Parameter: A = 0.5, f = 1, D = 0.1, c = 0.5, l = 0.5

Map of (y'(t), y(t))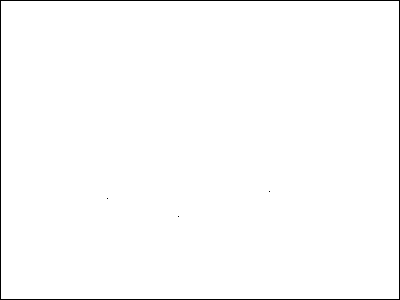

Poincare section

 

Further enlarging the driving force leeds again to another chaotic state at A = 0.55:

Parameter: A = 0.55, f = 1, D = 0.1, c = 0.5, l = 0.5

Map of (y'(t), y(t))

Poincare section [Click to enlarge]

The Attractor

In the section "Route to Chaos" you have seen the chaotic attractor for an amplitude of the driving force of A = 0.255. Here is a further look on its characteristics. Please click on the gray areas to see a more detailed picture:

Parameter: A = 0.255, f = 1, D = 0.1, c = 0.5, l = 0.5

Animations

Here you can see animations of two different chaotic attractors of the system. How is this done:
The poincare section depends on the phase shift Psi between the poincare section and the driving force. Here you can see the poincare section at Psi = 0:

Parameter: A = 0.255, f = 1, D = 0.1, c = 0.5, l = 0.5

Click to enlarge

Here is the poicare section with a phase shift of Pi/2. You get a slightly different picture of the attractor:

Parameter: A = 0.255, f = 1, D = 0.1, c = 0.5, l = 0.5

Click to enlarge

And finally for a phase shift of Pi:

Parameter: A = 0.255, f = 1, D = 0.1, c = 0.5, l = 0.5

Click to enlarge

The actual animation is now produced by showing the poincare sections with constantly changing phase shifts (0 ... 2 Pi). Here is the animation for A = 0.255. Look especially at the squeezing and folding of the attractor, which is the reason for the expontially divergence of two neighboring trajectories:

Parameter: A = 0.255, f = 1, D = 0.1, c = 0.5, l = 0.5

And here is the animation for A = 0.55:

Parameter: A = 0.23, f = 1, D = 0.1, c = 0.5, l = 0.5

References

[1] W. F. Schurawlew & D. M. Klimow, Applied methods in the theory of oscillations, Nauka Moskow 1988 (in russian)